Overview of the epitrix package

Thibaut Jombart

2019-05-13

epitrix implements small helper functions usefull in infectious disease modelling and epidemics analysis. This vignette provides a quick overview of the package’s features.

What does it do?

The main features of the package include:

  • gamma_shapescale2mucv: convert shape and scale of a Gamma distribution to mean and CV

  • gamma_mucv2shapescale: convert mean and CV of a Gamma distribution to shape and scale

  • gamma_log_likelihood: Gamma log-likelihood using mean and CV

  • r2R0: convert growth rate into a reproduction number

  • lm2R0_sample: generates a distribution of R0 from a log-incidence linear model

  • fit_disc_gamma: fits a discretised Gamma distribution to data (typically useful for describing delays)

  • hash_names: generate unique, anonymised, reproducible labels from various data fields (e.g. First name, Last name, Date of birth).

Fitting a gamma distribution to delay data

In this example, we simulate data which replicate the serial interval (SI), i.e. the delays between primary and secondary symptom onsets, in Ebola Virus Disease (EVD). We start by converting previously estimates of the mean and standard deviation of the SI (WHO Ebola Response Team (2014) NEJM 371:1481–1495) to the parameters of a Gamma distribution:

The shape and scale are parameters of a Gamma distribution we can use to generate delays. However, delays are typically reported per days, which implies a discretisation (from continuous time to discrete numbers). We use the package distcrete to achieve this discretisation. It generates a list of functions, including one to simulate data ($r), which we use to simulate 500 delays:

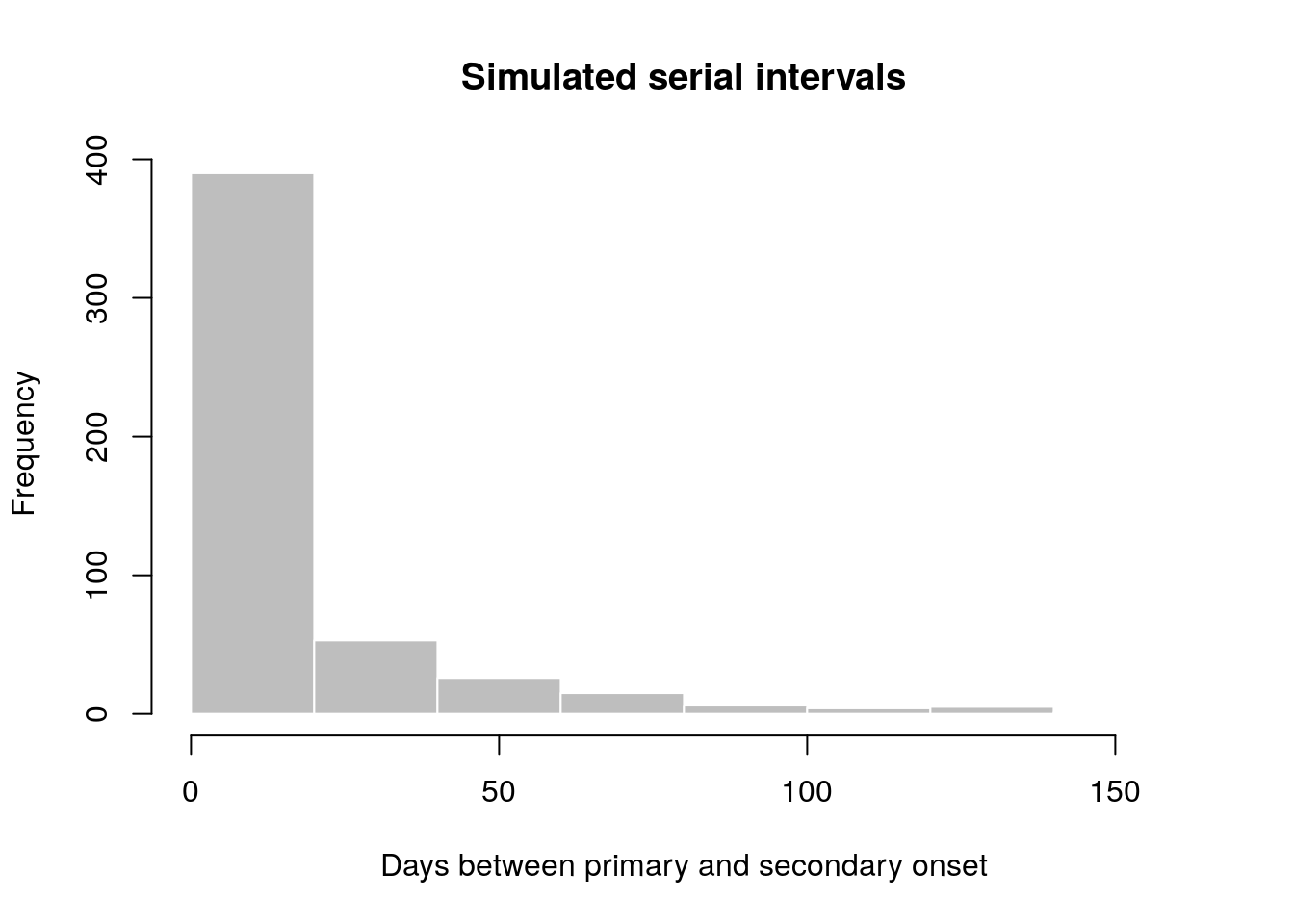
x contains simulated data, for illustrative purpose. In practice, one would use real data from an ongoing outbreaks. Now we use fit_disc_gamma to estimate the parameters of a dicretised Gamma distribution from the data:

Converting a growth rate (r) to a reproduction number (R0)

The package incidence can fit a log-linear model to incidence curves (function fit), which produces a growth rate (r). This growth rate can in turn be translated into a basic reproduction number (R0) using r2R0. We illustrate this using simulated Ebola data from the outbreaks package, and using the serial interval from the previous example:


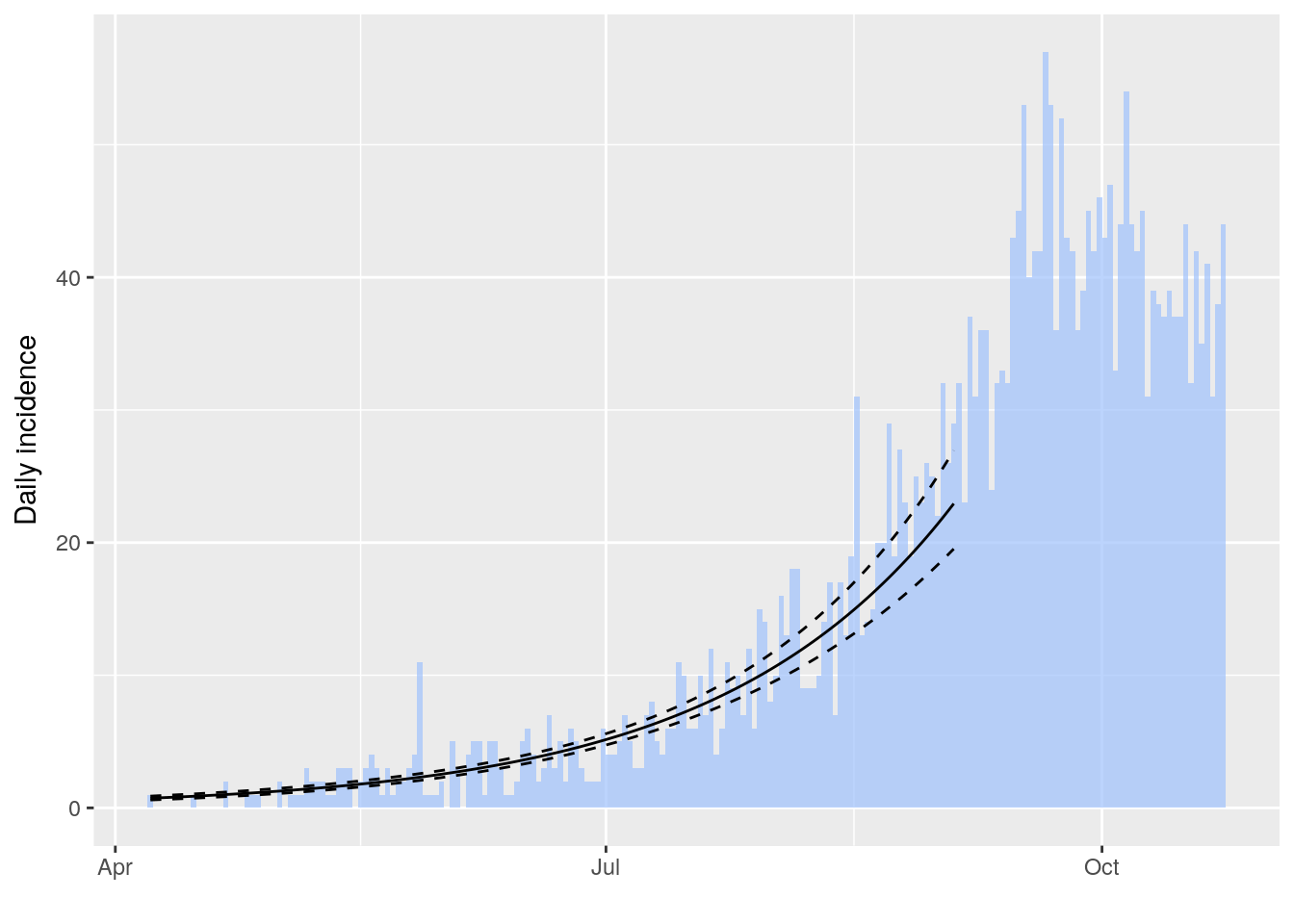
r2R0(f$info$r, si$d(1:100))
#> [1] 1.358887
r2R0(f$info$r.conf, si$d(1:100))
#>         2.5 %   97.5 %
#> [1,] 1.328372 1.388925

In addition, we can also use the function lm2R0_sample to generate samples of R0 values compatible with a model fit:


R0_val <- lm2R0_sample(f$model, si$d(1:100), n = 100)
head(R0_val)
#> [1] 1.360925 1.357800 1.360150 1.367461 1.352716 1.352790
hist(R0_val, col = "grey", border = "white")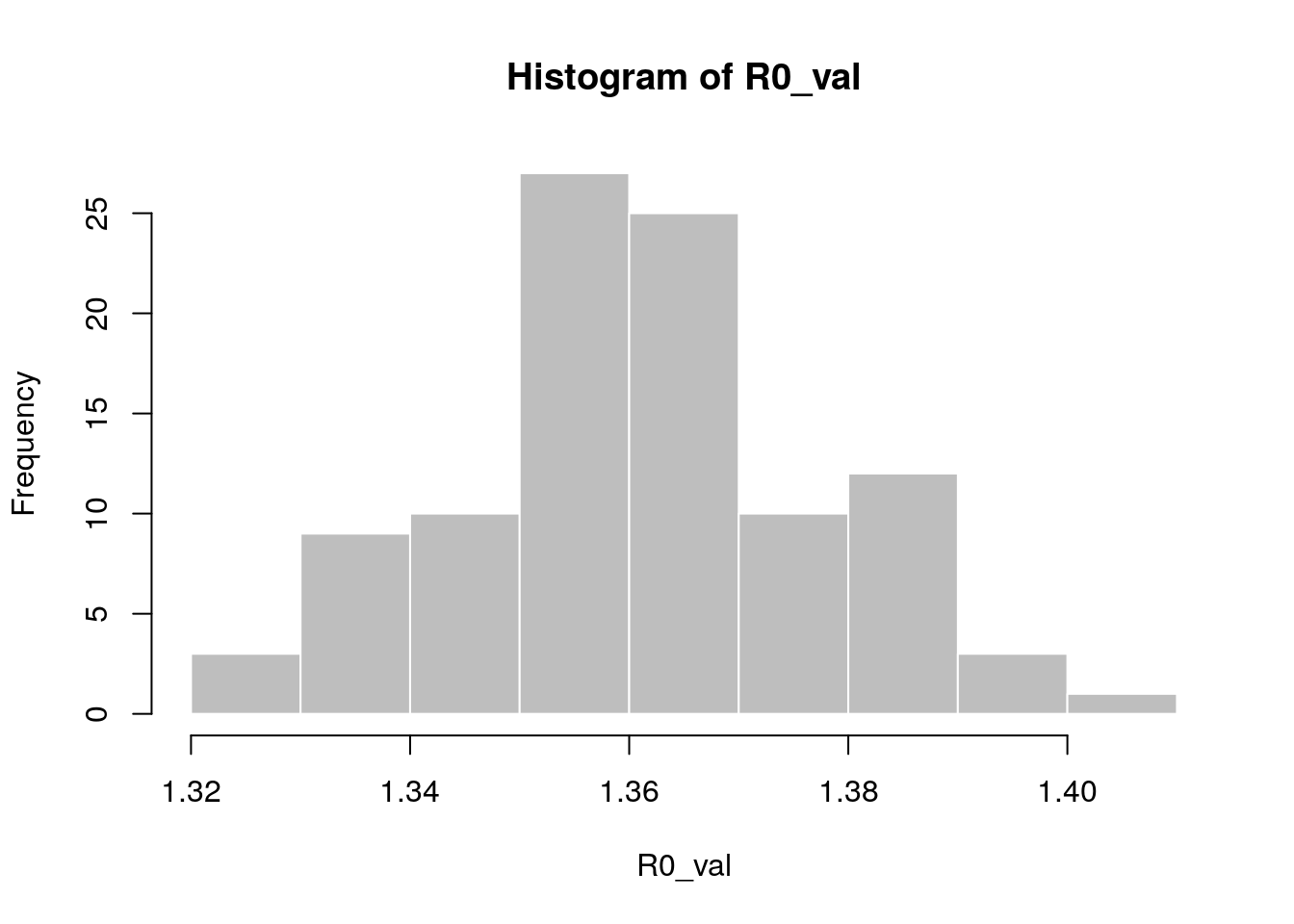

Standardising labels

If you want to use labels that will work across different computers, independent of local encoding and operating systems, clean_labels will make your life easier. The function transforms character strings by replacing diacritic symbols with their closest alphanumeric matches, setting all characters to lower case, and replacing various separators with a single, consistent one.

For instance:

If you happen to have informative labels in your data that are not alphanumeric, you will want to protect them with the protect argument:

vars <- c("Death in Structure  > 4h", "death in Structure < 4h")
clean_labels(vars, protect = "><")
#> [1] "death_in_structure_>_4h" "death_in_structure_<_4h"

If you don’t use the protect = "><", the two variables above would appear to be exactly the same.

Anonymising data

hash_names can be used to generate hashed labels from linelist data. Based on pre-defined fields, it will generate anonymous labels. This system has the following desirable features:

  • given the same input, the output will always be the same, so this encoding system generates labels which can be used by different people and organisations

  • given different inputs, the output will always be different; even minor differences in input will result in entirely different outputs

  • given an output, it is very hard to infer the input (it requires hacking skills); if security is challenged, the hashing algorithm can be ‘salted’ to strengthen security